七巧板

1、七巧板是一种拼板玩具，它是由宋代的宴几演变而来的，原为文人的一种室内游戏，后在民间演变为拼图板玩具。据清代陆以湉《冷庐杂识》说：：宋黄伯思宴几图，以方几七，长段相参，衍为二十五体，变为六十八名。明严瀓蝶几图，则又变通其制，以勾股之形，作三角相错形，如蝶翅。其式三，其制六，其数十有三，其变化之式，凡一百有余。近又有七巧图，其式五，其数七，其变化之式多至千余。体物肖 形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之。”

引发这个点子的人是北宋进士黄伯思，他先设计了六件长方形案几，于宴会时能视宾客多寡适当调整位置，随后又增加一件小几，七件案几全拼一起，会变成一个大长方形，分开组合可变化无穷。已和现代七巧板相差无几了。后来，明朝戈汕依照「燕几图」的原理，又设计了「蝶翅几」，由十三件不同的三角形案几而组成的，拼在一起是一只蝴蝶展翅的形状，分开后则可拼成出一百多种图形。七巧板- 现代的七巧板就是在「宴几图」与「蝶翅几」的基础上加以发展出来的。利用七巧板可以阐明若干重要几何关系，其原理便是古算术中的“出入相补原理”。

2、我们学习的乘法口诀，在我国二千多年前就有了。那时把口诀刻在“竹木简”上，是从“九九八十一”开始的。所以也叫“九九歌”。七百多年前才倒过来，从“一一得一”开始。远在春秋战国时代，九九歌就已经广泛地被人们利用着。在但是的许多著作中，已经引用部分乘法口诀。最初的九九歌是以“九九八十一”起到“二二如四”止，共36句口诀。发掘出的汉朝“竹木简”以及敦煌发现的古“九九术残木简”上都是从“九九八十一”开始的。“九九”之名就是取口诀开头的两个字。大约公元5～10世纪间，“九九”口诀扩充到“一一如一”。大约在宋朝（公元11、12世纪），九九歌的顺序才变成和现代用的一样，即从“一一如一”起到“九九八十一”止。元朱世杰著《算学启蒙》一书所载的45句口诀，已是从“一一”到”九九“，并称为九数法。现在用的乘法口诀有两种，一种是45句的，通常称为小九九；还有一种是81句的，通常称为大九九。书中记载，大九九最早见于清陈杰著的《算法大成》。

3、指南针由司南演变而来，S表示南，N表示北。指南针是我国古代四大发明之一，它是一种指示方向的工具。指南针，指南针又称司南，主要组成部分是一根装在轴上的磁针，磁针在天然地磁场的作用下可以自由转动并保持在磁子午线的切线方向上，磁针的北极指向地理的北极，利用这一性能可以辨别方向。常用于航海、大地测量、旅行及军事等方面。物理上指示方向的指南针的发明有三类部件，分别是司南、罗盘和磁针，均属于中国的发明。 据《古矿录》记载指南针最早出现于战国时期的磁山一带。

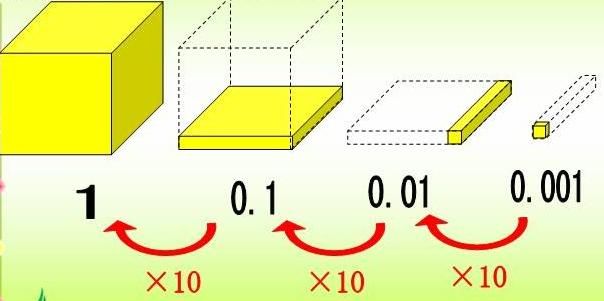
4、小数是我国最早提出和使用的。早在公元三世纪，我国古代数学家刘徽在解决一个数学难题时就提出了把整数个位以下无法标出名称的部分称为微数。小数的名称是公元十三世纪我国元代数字家朱世杰提出的。大约公元1300年，元朝刘瑾将小数的小数部分降低一行来记，这是世界上最早的小数表示法。如把63.12写成┻|||_||。

5、算筹是我国古代劳动人民发明的一种记数和计算的工具。算筹是用竹子或其他材料做成的小棒，用它表示不同数目。用算筹进行计算，简称“筹算”。几百年前，我国劳动人民根据古代的“筹算”发明了一种更加简便的计算工具——算盘。用算盘进行计算，简称“珠算”。算盘，是我国古代发明创造的重要成就之一，至今已有一千多年的历史了。我国是世界上发明算盘最早的国家。算盘，是由古代的“筹算”演变而来的。 “筹算”就是运用“筹码”——一种削制竹签来进行运算。唐代末年开始用“筹算”乘除法，到了宋代产生了“筹算”的除法歌诀，明代数学家吴敬著《算法十全》中，已正式有了“算盘”这一名称。约在明代初年，算盘逐渐流行，而论述算盘的著作，在十五世纪中叶已经很多了。由于珠算口诀便于记忆，运算方便，遂在我国普遍应用。同时，也陆续传到了日本，朝鲜、印度、美国、东南亚等国家，受到广泛欢迎。

6、我国古代早就运用方程的思想方法解决实际问题。早在700多年前，我国数学家李治（1192—1279）在解决问题的过程中，系统的应用并开发了“天元术”。14世纪初，我国数学家朱世杰又创立了“四元术”，这是我国古代数学的一次飞跃。

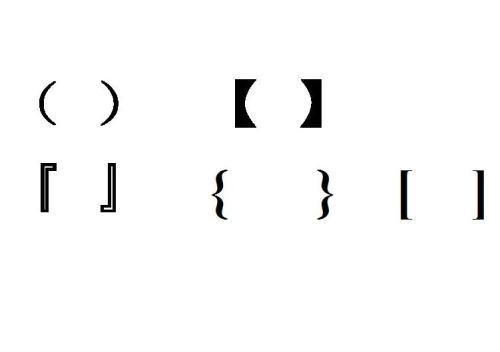
7、（ ）是小括号，又称为圆括号，是公元17世纪由荷兰人吉拉特首先使用的。[ ]是中括号，又称为方括号。17世纪，英国数学家瓦里士在计算时最先采用了它。{ }是大括号，又称为花括号，它约是在1593年由法国数学家韦达首先使用的。

8、数学家笛卡尔发明了数对。笛卡尔是著名的法国哲学家，科学家和数学家。三百多年前，笛卡尔第一个提出用x、y、z代表未知数，才形成现在的的方程。

9、最早有意识的系统使用字母来表示数的是法国数学家韦达。

10、在我国古代的数学名著《九章算术》里，记载着一种求最大公因数的方法——“以少减多，更相减损”。大约在公元前300年，古希腊的大数学家欧几里得把这样的计算方法称为“辗转相除法”。2000多年前，我国的数学名著《九章算术》中记载着有关土地面积计算的内容，具体介绍了各种图形的面积计算方法。著名数学家刘徽在注文中用“以盈补虚”的方法加以证明，并配有生动形象的图。

11、陈景润在攻克世界数学难题（哥德巴赫猜想）上取得了国际领先水平的成果，1966年陈景润证明了"1+2"成立（国际上称为陈式定理），即"任何一个大于2的偶数都可表示成一个素数与另一个素因子不超过2个的数之和"。对他成长成功帮助最大的是我国世界一流的数学家华罗庚。1956年，王元证明了“3+4”；同年，原苏联数学家阿·维诺格拉朵夫证明了“3+3”；1957年，王元又证明了“2+3”；潘承洞于1962年证明了“1+5”；1963年，潘承洞、巴尔巴恩与王元又都证明了“1+4”。

12、传说远在四千五百年前，我们的祖先就用一种滴水的器具来计时，名叫刻漏，它是一种水钟。

13、符号“+、—”是五百年前一位德国人最先使用的。乘号“×”是在17世纪由英国数学家欧德莱最先使用的除号“÷”是三百多年前一位瑞士数学家最先使用的，用一条横线把两个圆点分开，恰好表示了平均分的意思。

14、我们经常使用的数字0、1、2、3、4、5、6、7、8、9，最早是印度人发明的，大约1200年前传到阿拉伯，约800年前又传到欧洲。欧洲人把这些数字叫阿拉伯数字。

15、大约在公元100年，我国数学名著《九章算术》中就明确提出负数的概念，以及正、负数的意义。到公元3世纪，我国著名数学家刘徽更加明确了负数的意义。在算筹中，刘徽把两种表示相反意义的算筹叫做正数和负数。正数和负数这一对概念在我国沿用至今，已有两千年的历史。它是我国古代数学家对人类数学发展的重大贡献之一，在西方，负数直到17世纪才被人们承认。

16、我国是世界上最早使用四舍五入法进行计算的国家，大约一千七百多年前天文学家杨伟明确提出了“四舍五入法”。

17、《孙子算经》记载:今有物不知其数，三三数之余二，五五数之余三，七七数之余二，问物几何？它的意思是：有一些物品，如果3个3个地数，最后剩2个，如果5个5个地数，最后剩3个，如果7个7个地数，最后剩2个。求这些物品一共有多少？这个问题人们通常把它叫做“孙子问题”，西方数学家把它称为“中国剩余定理”。

18、圆周率，古希腊大数学家阿基米德(公元前287–212 年) 开创了人类历史上通过理论计算圆周率近似值的先河。阿基米德从单位圆出发，先用内接正六边形求出圆周率的下界为3，再用外接正六边形并借助勾股定理求出圆周率的上界小于4。接着，他对内接正六边形和外接正六边形的边数分别加倍，将它们分别变成内接正12边形和外接正12边形，再借助勾股定理改进圆周率的下界和上界。他逐步对内接正多边形和外接正多边形的边数加倍，直到内接正96边形和外接正96边形为止。最后，他求出圆周率的下界和上界分别为223/71 和22/7， 并取它们的平均值3.141851 为圆周率的近似值。阿基米德用到了迭代算法和两侧数值逼近的概念，称得上是“计算数学”的鼻祖。中国古算书《周髀算经》（约公元前2世纪）的中有“径一而周三”的记载，意即取π=3。

汉朝时，张衡得出π=3.162。这个值不太准确，但它简单易理解。公元263年，中国数学家刘徽用“割圆术”计算圆周率，他先从圆内接正六边形，逐次分割一直算到圆内接正192边形。他说“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”，包含了求极限的思想。刘徽给出π=3.141024的圆周率近似值。

公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927。在之后的800年里祖冲之计算出的π值都是最准确的。